Warrant Tutorial
Introduction
A warrant confers the right to buy (call-warrant) or sell (put-warrant) a specific quantity of a specific underlying instrument at a specific price over a specific period of time.
Pay-out Profile
With some warrants, the option right can only be exercised on the expiration date. These are referred to as “European-style” warrants. With “American-style” warrants, the option right can be exercised at any time prior to expiration. The vast majority of listed warrants are cash-exercised, meaning that you cannot exercise the warrant to obtain the underlying physical share. The exception to this rule is Switzerland, where physically settled warrants are widely available.
IBKR does allow for US and Canadian warrant exercise. Customers wishing to do so should submit a Customer Service ticket stating the name/symbol of the warrant, the quantity of shares and the intended action (i.e. exercise). The broker will pass through all associated exercise costs to the customer upon completion of the request. US or Canadian warrants are not eligible for auto-exercise at expiration. Warrants remaining in an account at expiration will be removed as worthless.
Factors that influence pricing
Not only do changes in the price of the underlying instrument influence the value of a warrant, a number of other factors are also involved. Of particular importance to investors in this regard are changes in volatility, i.e. the degree to which the price of the underlying instrument fluctuates. In addition, changes in interest rates and the anticipated dividend payments on the underlying instrument also play a role.
However, changes in implied volatility - as well as interest rates and dividends - only affect the time value of a warrant. The primary driver - intrinsic value - is solely determined by the difference between the price of the underlying instrument and the specified exercise price.
Historical and implied volatility
In addressing this topic, a differentiation has to be made between historical and implied volatility. Implied volatility reflects the volatility market participants expect to see in the financial instrument in the days and months ahead. If implied volatility for the underlying instrument increases, so does the price of the warrant.
This is because the probability of profiting from a warrant during a particular time-frame increases if the price of the underlying instrument is highly volatile. The warrant is therefore more valuable.
Conversely, if implied volatility decreases, that leads to a decline in the value of warrants and hence occasionally to nasty surprises for warrant investors who aren’t familiar with the concept and influence of volatility.
Interest rates and dividends
Issuers hedge themselves against price changes in the warrant through purchases and sales of the underlying instrument. Due to the leverage afforded by warrants, the issuer needs considerably more capital to hedge its exposure than you require to buy the warrants. The issuer’s interest expense associated with that capital is included in the price of the warrant. The amount of embedded interest reduces over time and at expiration is zero.
In the case of puts, the situation is exactly the opposite. Here, the issuer sells the underlying instrument
short to establish the necessary hedge, and in so doing receives capital that can earn interest. Thus interest reduces the price of the warrant by an amount that decreases over time.
As the issuer owns shares as a part of its hedging operations, it is entitled to receive the related dividend
payments. That additional income reduces the price of call warrants and increases the price for puts. But if the dividend expectations change, that will have an influence on the price of the warrants. Unanticipated special dividends on the underlying instrument can lead to a price decline in the related warrants.
Key valuation factors
Let’s assume the following warrant:
Warrant Type: Call
Term to expiration: 2 years
Underlying : ABC Share
Share price: EUR 30.00
Strike: EUR 30.00
Exercise ratio: 0.1
Warrant’s price: EUR 0.30
Intrinsic value
Intrinsic value represents the amount you could receive if you exercised the warrant immediately and then bought (in the case of a call) or sold (put) the underlying instrument in the open market.
It’s very easy to calculate the intrinsic value of a warrant. In our example the intrinsic value is EUR 00.00
and is calculated as follows:
(price of underlying instrument – strike price) x exercise ratio
= (EUR 30.00 – EUR 30.00) x 0.1
= EUR 00.00
If the price of the ABC share increases by EUR 1, the intrinsic value becomes
= (EUR 31.00 – EUR 30.00) x 0.1
= EUR 00.10
The intrinsic value of a put warrant is calculated with this formula:
(strike price – price of underlying instrument) x exercise ratio
It’s important to note that the intrinsic value of a warrant can never be negative. By way of explanation:
if the price of the underlying instrument is at or below the exercise price, the intrinsic value of a call equals zero. In this instance, the price of the warrant consists only of “time value”. On the flipside, the intrinsic value of a put is equal to zero if the price of the underlying instrument is at or above the exercise price.
Time value
Once you’ve calculated the intrinsic value of a warrant, it’s also easy to figure out what the time value of that warrant is. You simply deduct the intrinsic value from the current market price of the warrant. In our example, the time value is equal to EUR 1.30 as you can see from the following calculation:
(warrant price – intrinsic value)
= (EUR 0.30 EUR – EUR 0.00)
= EUR 0.30
Time value gradually erodes during the term of a warrant and ultimately ends up at zero upon expiration. At that point, warrants with no intrinsic value expire worthless. Otherwise you can expect to receive payment of the intrinsic value. Take note, though: a warrant’s loss of time value accelerates during the final months of its term.
Premium
The premium indicates how much more expensive a purchase/sale of the underlying instrument would be via the purchase of a warrant and the immediate exercise of the option right as opposed to simply buying/selling the underlying instrument in the open market.
Hence the premium is a measure of how expensive a warrant actually is. It follows that, when given a choice between warrants with similar features, you should always buy the one with the lowest premium. By calculating the premium as an annualized percentage, warrants with different terms to expiry can be compared with each other.
The percentage premium for the call warrant in our example can be calculated as follows:
(strike price + warrant price / exercise ratio – share price) / share price * 100
= (EUR 30.00 + EUR 0.30 / 0.1 – EUR 30.00) / EUR 30.00 x 100
= 10 percent
Leverage
The amount of leverage is the price of the share * ratio divided by the price of the warrant. In our example 30.00*0.1/0.3 = 10. So when the price of ABC increases by 1% the value of the warrant increases by 10%.
The amount of leverage is not constant however; it varies as intrinsic and time value changes, and is particularly sensitive to changes in intrinsic value. As a rule of thumb, the higher the intrinsic value of the warrant, the lower the leverage. For example (assuming constant time value):
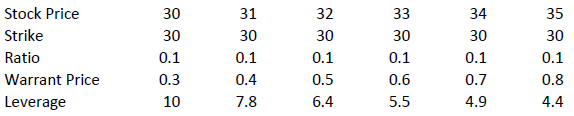
Knock-out (Turbo) Tutorial
Introduction
Knock-out warrants (turbos), like vanilla warrants, derive their value from the difference between the price of the underlying and the strike. They differ significantly however from vanilla warrants in many important respects:
- They can expire (knock-out) prematurely if the price of the underlying instrument touches or falls below (in the case of knock-out calls) or exceeds (in the case of knockout puts) a predetermined barrier-level. It expires worthless if the barrier equals the strike, or it may have a residual stop-loss value if the barrier is set higher than the strike (in the case of a call).
- Changes in implied volatility have little or no impact on knock-out products, therefore their pricing is easier for investors to comprehend than that of warrants.
- They have little or no time value (because of the presence of the knock-out barrier), and therefore have a higher degree of leverage than a warrant with the same strike. This is because the absence of time value makes the instrument “cheaper”.
Pay-out Profile
Leverage
As discussed above, knock-out warrants exhibit high degrees of leverage, particularly as the price of the underlying nears the strike/barrier. Consider the following example of a long turbo on the Dow Jones Index, compared to a vanilla warrant:
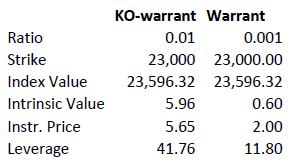
Intrinsic value = (index value – strike) x ratio
Leverage = Index Value x Ratio / Instrument Price
A vanilla warrant retains significant time value even as the underlying price approaches the strike, sharply reducing its leverage compared to a knock-out warrant.
Product types
As discussed above, the barrier may either equal the strike, or be set above (calls) or below (puts). In the latter cases a small residual value remains after knock-out, corresponding to the difference between the barrier (the stop-loss level) and the strike.
Moreover, knock-out products may either have an expiration date or may be open-ended. This makes a difference in the way interest is accounted for. If the contract has an expiration date interest is included in the premium, the amount of which reduces over time and is zero on expiration. This is analogous to a standard vanilla warrant.
in relation to an expiration date. The price of the contract therefore corresponds exactly to its intrinsic value. Interest however must be accounted for. This is done by a daily adjustment of the barrier and strike. The following example shows the daily adjustment for a long open-end turbo on the Dow Jones Index:
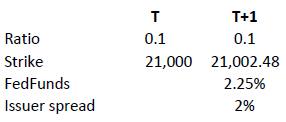
The adjustment = Strike T x (1+ FedFunds/360 + Issuer Spread/360).
The intrinsic value of the instrument is correspondingly reduced as follows, assuming no change in the value of the DJ Index):
Intrinsic value = (index value – strike) x ratio
Discount Certificates Tutorial
Introduction
Discount certificates are designed to provide an enhanced return in sideways markets, compared to a direct investment in the underlying.
Discount certificates make it possible for you to buy an underlying instrument for less than its current market price. However, the maximum payback on a discount certificate is limited to a predetermined amount (cap).
Discount certificates normally have a term to maturity of one to three years. At maturity, a determination is made of where the price of the underlying instrument stands.
If it is at or above the cap, you’ll earn the maximum return and receive payment of the amount reflected by the cap.
If the price of the underlying instrument is below the cap on the maturity date, you’ll receive either the corresponding number of shares or a cash settlement reflecting the value of the underlying instrument on the maturity date.
Pay-out Profile
Example
Assume a discount certificate on ABC share. The certificate has a cap of EUR 40.00, and a purchase price of EUR 36.00. The table below shows scenarios depending on the final price of the underlying.
Factor Certificates Tutorial
Introduction
Factor certificates employ a daily leverage factor that multiplies the daily performance of the underlying instrument. Unlike knock-out warrants and mini-futures, factor certificates do not have a knock-out barrier. To avoid a loss greater than the investment, the calculation resets intraday if the performance of the underlying threatens to render the certificate worthless.
Daily Leverage
The performance of the certificate is calculated daily, without reference to previous days’ values. If the underlying returns 1% on the day, the value of 3x certificate increases by 3%, a 5x by 5%. The next day the process is repeated, referencing the prior day’s underlying close.
As such, factor certificates are particularly suitable for day-traders.
However, for a period of more than one day, the cumulative performance of the underlying cannot be simply multiplied by a factor of 3 as the previous day’s price always forms the new basis of calculating each day’s performance for the certificate. To illustrate with an example:
Cumulatively, the factor certificate has returned less than 3x the performance of the underlying.
Intraday Reset
If an underlying for a factor certificate loses more than a certain percentage of its value intraday, the calculation is reset by simulating a new day. The reset threshold varies depending on the leverage factor.
Let’s assume a long factor certificate with a 10x leverage factor. According to the terms of the certificate, a reset will be triggered if the underlying loses more than 9.5% during the calculation day.
Let’s now assume that the underlying loses 12% of its value during a particular day. The reset
and final performance will be as follows:
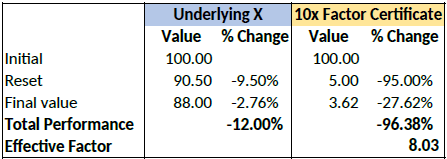
Complex Position Size
For complex, multi-leg options positions comprising two or more legs, TWS might not track all changes to this position, e.g. a vertical spread where the short leg is assigned and the user re-writes the same leg the next day, or if the user creates a the position over multiple trades, or if the order is not filled as a native combination at the exchange.
If you received a message because you are submitting an order to close a position, roll a position, or modify a position using the “% Change” feature, it means that the maximum quantity of option positions in your account that are available to close for this order is different from that of the original position tracked by TWS.
Before submitting, you should review the order and confirm that the order quantity we have calculated is the correct quantity that you want to trade.
SMAとそのしくみ
概観:
SMAとは「Special Memorandum Account」のことです。この口座に保有されるのは株式や現金ではなく、Reg. Tの信用取引口座にある有価証券の時価が上昇したときに発生する信用枠を指します。SMAの目的は含み益による次の買い付けのために買付力を維持することにあります。これができない場合には次の買付の際に余剰の株式を取りくずして資金化することになるため、SMAは安定した口座価値を維持し、不必要な資金調達取引を最小限に抑えるのに役立ちます。
有価証券の価値が上昇するとSMAも上昇しますが、 有価証券の価値が下がる場合でもSMAが下がることはありません。SMAが減少するのは有価証券を購入したり現金を引き出す場合のみであり、SMAの使用に関する唯一の制限は、追加の購入や引出しによって口座が維持証拠金額の要件を下回らないことになります。SMAを増加させる取引には、現金預金、受取利息、または受取配当金（1ドル単位）、有価証券の売却（純収入の50%）などがあります。注意すべき点は、SMA残高は過去の記帳項目をすべてを集計したものであり、口座開設時からの残高に影響を与えるということです。長期間分の大量のエントリーが含まれているため、日々のアクティビティステートメントから現在のSMAのレベルを計算し確認することは、可能ではあるものの現実的には困難です。
SMAがどのように機能するか、例を使って考えてみます。ある口座保有者が$5,000を入金し、ローンバリューが50%の有価証券を$10,000購入したと仮定します（または必要証拠金が1-ローンバリュー、または50%に等しいとします）。この場合、口座開設前と開設後の値は以下のようになります:
|
項目
|
詳細
|
イベント1 - 初回入金
|
イベント2 - 株式購入
|
|
A.
|
キャッシュ
|
$5,000
|
($5,000)
|
|
B.
|
ロング株式市場価格
|
$0
|
$10,000
|
|
C.
|
流動性総資産/EWL* (A + B)
|
$5,000
|
$5,000
|
|
D.
|
委託証拠金（B * 50%）
|
$0
|
$5,000
|
|
E
|
委託証拠金余力（C - D）
|
$5,000
|
$0
|
|
F.
|
SMA
|
$5,000
|
$0
|
|
G.
|
購買力
|
$10,000
|
$0
|
次に、買い持ち銘柄の価値が$12,000に上昇したとします。この$2,000の市場価格の上昇により、$1,000のSMAが発生し、口座保有者は次のうちのいずれかが可能となります: 1）追加の資金を預けることなく、50%の証拠金率を想定して$2,000の価値のある有価証券を追加で購入する。または、2）現金で$1,000を引出す（口座に現金がない場合には、借方の残高を増やすことで資金を調達することができます）。以下をご覧ください:
|
項目
|
詳細
|
イベント2 – 株式購入
|
イベント3 - 株価上昇
|
|
A.
|
キャッシュ
|
($5,000)
|
($5,000)
|
|
B.
|
ロング株式市場価格
|
$10,000
|
$12,000
|
|
C.
|
流動性総資産/EWL* (A + B)
|
$5,000
|
$7,000
|
|
D.
|
委託証拠金（B * 50%）
|
$5,000
|
$6,000
|
|
E
|
委託証拠金余力（C - D）
|
$0
|
$1,000
|
|
F.
|
SMA
|
$0
|
$1,000
|
|
G.
|
購買力
|
$0
|
$2,000
|
*EWLは貸付金額を含む資産価値のことであり、この例では流動性資産を指します。
SMAはReg. Tに基づく考え方です。IB LLCの証券口座がオーバーナイトの必要証拠金を遵守していることを確認するために使用されるものであり、日中やオーバーナイトの維持証拠金に対する遵守の確認をするためには使用されません。また、コモディティ口座の証拠金遵守の確認に使用されることもありません。同様に、オーバーナイトつまりReg. T必要証拠金が必要となる時間（米国東部標準時15:50）にSMAがマイナスである口座は、Reg. T必要証拠金遵守のため、ポジションの強制決済の対象となります。
流動性の追加と削除
概観:
この記事は個別の手数料体系を利用する際の、取引所手数料および流動性追加および削除手数料の理解を目的としています。
流動性の追加と削除は、株式および株式/指数オプションの両方に適用されるコンセプトです。ある注文が流動性を追加または削除するかは、その注文が約定の付くものであるかないかによります。
約定の付く注文は流動性を下げます。
約定の付く注文とは成行注文、もしくは指値が現在の市場価格かまたはそれ以上/以下になる、買い/売りの指値注文を指します。
1. 約定の付く買いの指値注文の場合、指値価格はアスク以上となります。
2. 約定の付く売りの指値注文の場合、指値価格はビッド以下となります。
例:
XYZ株の現在のアスク（オファー）サイズ/価格は、46.00で400株です。100 XYZ株 @ 46.01で、買いの指値注文を発注します。この注文はすぐに約定可能なため、約定が付くとみなされます。 流動性を下げるにあたって取引所手数料が発生する場合、これがお客様に請求されます。
約定の付かない注文は流動性を追加します。
約定の付かない注文とは、指値価格が現在の市場価格以下/以上の買い/売りの指値注文を指します。
1. 約定の付かない買いの指値注文の場合、指値価格はアスク以下となります。
2. 約定の付かない売りの指値注文の場合、指値価格はビッド以上となります。
例:
XYZ株の現在のアスク（オファー）サイズ/価格は、46.00で400株です。100 XYZ株 @ 45.99で、売りの指値注文を発注します。この注文はすぐに約定はせずに最良ビッドとして市場に出されるため、約定が付かないとみなされます。
お客様の指値注文を約定させる結果となる約定性のある売り注文を誰かが発注した場合、流動性追加手数料があればお客様にリベート（クレジット）が発生します。
留意点:
1. オプション取引をする口座はすべて、オプション取引所による流動性削除/追加手数料またはクレジットの対象となります。
2. 弊社のウェブサイトにおいては、流動性削除/追加体系内で負数のものだけが、リベート（クレジット）となります。
https://www.interactivebrokers.co.jp/jp/index.php?f=2763
約定の付かない注文とは、指値価格が現在の市場価格以下/以上の買い/売りの指値注文を指します。
1. 約定の付かない買いの指値注文の場合、指値価格はアスク以下となります。
2. 約定の付かない売りの指値注文の場合、指値価格はビッド以上となります。
例:
XYZ株の現在のアスク（オファー）サイズ/価格は、46.00で400株です。100 XYZ株 @ 45.99で、売りの指値注文を発注します。この注文はすぐに約定はせずに最良ビッドとして市場に出されるため、約定が付かないとみなされます。
お客様の指値注文を約定させる結果となる約定性のある売り注文を誰かが発注した場合、流動性追加手数料があればお客様にリベート（クレジット）が発生します。
留意点:
1. オプション取引をする口座はすべて、オプション取引所による流動性削除/追加手数料またはクレジットの対象となります。
2. 弊社のウェブサイトにおいては、流動性削除/追加体系内で負数のものだけが、リベート（クレジット）となります。
https://www.interactivebrokers.co.jp/jp/index.php?f=2763
上記のリンクは株式およびオプションの手数料/費用に関する参照となります。
米国オプションに対し異なる手数料請求が発生する理由
IBのオプション手数料の請求は、ふたつの要素から成り立っています:
1. 弊社に蓄積される約定手数料。 スマートルーティングされる注文への手数料はコントラクト1枚あたり$0.70に設定され、これは1ヶ月内の注文のコントラクトが100,000枚を超えた場合、コントラクト1枚あたり$0.15まで下がります（ダイレクトルーティングされる注文、プレミアムオプションに対するディスカウントレートおよび最低注文料金に関してはウェブサイトをご覧ください）、および
2. 第三者機関である取引所手数料、規制手数料および/または取引手数料。
第三者機関による手数料に関し、特定の米国オプション取引所では流動性手数料/リベート体系を設けています。これは弊社の約定手数料やその他の規制手数料/取引手数料と集約されると、注文によって異なるコントラクトあたりに請求される総合手数料となることがあります。 これは手数料の請求ではなく顧客への支払いに転じる可能性もある、取引所の計算部分に起因するものです。これには注文の特性や現行のビッド/アスクのクオートなど、弊社の範疇外となる要因が含まれます。
流動性手数料/リベートモデルに基いて運営している取引所では、流動性を移動する注文（約定の付く注文）に対しては手数料を請求し、流動性を追加する注文（約定の付かない指値注文）に対してはクレジットを提供します。手数料は取引所や顧客タイプ（一般、ブローカー・ディーラー、企業、マーケットメーカー、プロフェッショナルなど）、また一般の顧客に対し通常$0.10 - $0.42の範囲となるリベート（クレジット）、および$0.15 - $0.50の手数料のオプション原資産によって変わります。
弊社は約定の付くオプション注文を約定価格の一番良い取引所にルーティングするよう義務付けられており、どの取引所にルーティングをするかを決定するにあたって利用可能な市場が複数存在する場合、スマートルーターは流動性移動手数料も考慮の上で発注を行います。 このためスマートルーターは、市場が少なくとも$0.01（オプション乗数が標準の100の場合、$1.00の価格向上につながります）良くなる可能性がある場合には、手数料の一番高い取引所に成行注文のみをルーティングします。
流動性の追加/移動に関する詳細および例に関しましては、KB201をご参照ください。
Risks of Volatility Products
Trading and investing in volatility-related Exchange-Traded Products (ETPs) is not appropriate for all investors and presents different risks than other types of products. Among other things, ETPs are subject to the risks you may face if investing in the components of the ETP, including the risks relating to investing in complex securities (such as futures and swaps) and risks associated with the effects of leveraged investing in geared funds. Investors should be familiar with the diverse characteristics of each ETF, ETN, future, option, swap and any other relevant security type. We have summarized several risk factors (as identified in prospectuses for ETPs and in other sources) and included links so you can conduct further research. Please keep in mind that this is not a complete list of the risks associated with these products and investors are responsible for understanding and familiarizing themselves completely before entering into risk-taking activities. By providing this information, Interactive Brokers (IB) is not offering investment or trading advice regarding ETPs to any customer. Customers (and/or their independent financial advisors) must decide for themselves whether ETPs are an appropriate investment for their portfolios.
An ETP may not be benchmarked to the index it appears to track
"An investor should only consider an investment in a Fund if he or she understands the consequences of seeking exposure to VIX futures contracts. The Funds are benchmarked to the S&P VIX Short-Term Futures Index, an investable index of VIX futures contracts. The Funds are not benchmarked to the VIX Index. The VIX Index is a non-investable index that measures the implied volatility of the S&P 500. For these purposes, "implied volatility" is a measure of the expected volatility (i.e., the rate and magnitude of variations in performance) of the S&P 500 over the next 30 days. The VIX Index does not represent the actual volatility of the S&P 500. The VIX Index is calculated based on the prices of a constantly changing portfolio of S&P 500 put and call options. The Index underlying each Fund consists of short-term VIX futures contracts. As such, the performance of the Index and the Funds can be expected to be very different from the actual volatility of the S&P 500 or the performance of the VIX Index." [Page 1]
"… your ability to benefit from any rise or fall in the level of the VIX Index is limited. The Index underlying your ETNs is based upon holding a rolling long position in futures on the VIX Index. These futures will not necessarily track the performance of the VIX Index. Your ETNs may not benefit from increases in the level of the VIX Index because such increases will not necessarily cause the level of VIX Index futures to rise. Accordingly, a hypothetical investment that was linked directly to the VIX Index could generate a higher return than your ETNs." [Page PS-12]
ETPs may not provide a suitable hedge
"Historical correlation trends between the Index and other asset classes may not continue or may reverse, limiting or eliminating any potential diversification or other benefit from owning a Fund." [Page 20]
Volatility based ETPs are volatile in themselves and are not intended for long term investment
"… investments can be highly volatile and the Funds may experience large losses from buying, selling or holding such investments. ... In addition, gains, if any, may be subject to significant and unexpected reversals. The Funds generally are intended to be used only for short-term investment horizons. As with all investments, an investor in any of the Funds could potentially lose the full principal value of his/her investment, even over periods as short as one day." [Page 1]
"The ETNs are only suitable for a very short investment horizon. The relationship between the level of the VIX Index and the underlying futures on the VIX Index will begin to break down as the length of an investor’s holding period increases, even within the course of a single Index Business Day. ... The ETNs are not long term substitutes for long or short positions in the futures underlying the VIX Index. ... The long term expected value of your ETNs is zero. If you hold your ETNs as a long term investment, it is likely that you will lose all or a substantial portion of your investment. " [Page PS-15]
The use of leveraged positions could result in the total loss of an investment
"The Ultra Fund utilizes leverage in seeking to achieve its investment objective and will lose more money in market environments adverse to its respective daily investment objectives than funds that do not employ leverage…
For example, because the Ultra Fund includes a two times (2x) multiplier, a single-day movement in the Index approaching 50% at any point in the day could result in the total loss or almost total loss of an investor’s investment if that movement is contrary to the investment objective of the Fund, even if the Index subsequently moves in an opposite direction, eliminating all or a portion of the movement…
Inverse positions can also result in the total loss of an investor’s investment. For the Inverse Fund, a single-day or intraday increase in the level of the Fund’s benchmark approaching 100% could result in the total loss or almost total loss of an investor’s investment, even if such Fund’s benchmark subsequently moves lower. " [Page 14]
Possible illiquid markets may exacerbate losses
"Financial Instruments cannot always be liquidated at the desired price. It is difficult to execute a trade at a specific price when there is a relatively small volume of buy and sell orders in a market. A market disruption can also make it difficult to liquidate a position or find a swap counterparty at a reasonable cost. " [Page 17]
Short covering may intensify losses in volatility-related ETPs
In the event of a sudden market volatility change, many traders with positions in volatility-related products will incur substantial unexpected losses. These losses may cause them to choose to close their positions. The losses may also result in margin deficits and subsequent liquidations of some or all positions. Such closing trades will add to the movement of these products. Since speculative interest in the VIX is at an all-time high, there may be no precedent for what will happen if volatility moves quickly.
The Commodity Futures Trading Commission's (CFTC) weekly Commitments of Traders (COT) report provides a breakdown of the net positions for "non-commercial" (speculative) traders in U.S. futures markets. As of September 2017 CFTC reported VIX speculative net short is at an all-time high.
"Despite the fact that the average daily closing value of the CBOE Volatility Index (VIX) is about 11.5 so far this year, VIX futures and options both had record days for volume and for open interest this month. … VIX futures hit a new record for open interest with more than 673,000 contracts on August 7 (2017), and VIX options reached a new record for open interest with 14,783,380 contracts open on August 15 (2017)."
*As this data is constantly changing, investors in volatility-related products should regularly check for updates.
ETP issuers may redeem shares for cash in the event of extreme moves
"The Intraday Indicative Value on any Index Business Day could be reduced to 20% or less of the prior day’s Closing Indicative Value. If this occurs, we may choose to exercise our right to effect an Event Acceleration of the ETNs for an amount equal to that day’s Closing Indicative Value and you may not receive any of your initial investment." [Page PS-17]
