Warrant Tutorial
Introduction
A warrant confers the right to buy (call-warrant) or sell (put-warrant) a specific quantity of a specific underlying instrument at a specific price over a specific period of time.
Pay-out Profile
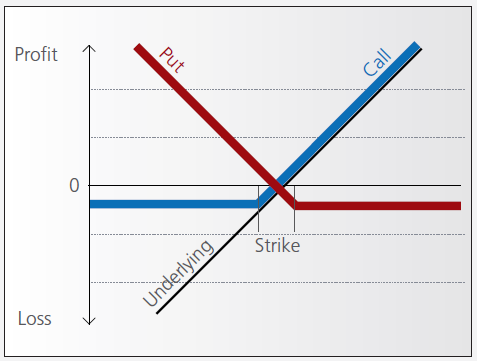
With some warrants, the option right can only be exercised on the expiration date. These are referred to as “European-style” warrants. With “American-style” warrants, the option right can be exercised at any time prior to expiration. The vast majority of listed warrants are cash-exercised, meaning that you cannot exercise the warrant to obtain the underlying physical share. The exception to this rule is Switzerland, where physically settled warrants are widely available.
Factors that influence pricing
Not only do changes in the price of the underlying instrument influence the value of a warrant, a number of other factors are also involved. Of particular importance to investors in this regard are changes in volatility, i.e. the degree to which the price of the underlying instrument fluctuates. In addition, changes in interest rates and the anticipated dividend payments on the underlying instrument also play a role.
However, changes in implied volatility - as well as interest rates and dividends - only affect the time value of a warrant. The primary driver - intrinsic value - is solely determined by the difference between the price of the underlying instrument and the specified exercise price.
Historical and implied volatility
In addressing this topic, a differentiation has to be made between historical and implied volatility. Implied volatility reflects the volatility market participants expect to see in the financial instrument in the days and months ahead. If implied volatility for the underlying instrument increases, so does the price of the warrant.
This is because the probability of profiting from a warrant during a particular time-frame increases if the price of the underlying instrument is highly volatile. The warrant is therefore more valuable.
Conversely, if implied volatility decreases, that leads to a decline in the value of warrants and hence occasionally to nasty surprises for warrant investors who aren’t familiar with the concept and influence of volatility.
Interest rates and dividends
Issuers hedge themselves against price changes in the warrant through purchases and sales of the underlying instrument. Due to the leverage afforded by warrants, the issuer needs considerably more capital to hedge its exposure than you require to buy the warrants. The issuer’s interest expense associated with that capital is included in the price of the warrant. The amount of embedded interest reduces over time and at expiration is zero.
In the case of puts, the situation is exactly the opposite. Here, the issuer sells the underlying instrument
short to establish the necessary hedge, and in so doing receives capital that can earn interest. Thus interest reduces the price of the warrant by an amount that decreases over time.
As the issuer owns shares as a part of its hedging operations, it is entitled to receive the related dividend
payments. That additional income reduces the price of call warrants and increases the price for puts. But if the dividend expectations change, that will have an influence on the price of the warrants. Unanticipated special dividends on the underlying instrument can lead to a price decline in the related warrants.
Key valuation factors
Let’s assume the following warrant:
Warrant Type: Call
Term to expiration: 2 years
Underlying : ABC Share
Share price: EUR 30.00
Strike: EUR 30.00
Exercise ratio: 0.1
Warrant’s price: EUR 0.30
Intrinsic value
Intrinsic value represents the amount you could receive if you exercised the warrant immediately and then bought (in the case of a call) or sold (put) the underlying instrument in the open market.
It’s very easy to calculate the intrinsic value of a warrant. In our example the intrinsic value is EUR 00.00
and is calculated as follows:
(price of underlying instrument – strike price) x exercise ratio
= (EUR 30.00 – EUR 30.00) x 0.1
= EUR 00.00
If the price of the ABC share increases by EUR 1, the intrinsic value becomes
= (EUR 31.00 – EUR 30.00) x 0.1
= EUR 00.10
The intrinsic value of a put warrant is calculated with this formula:
(strike price – price of underlying instrument) x exercise ratio
It’s important to note that the intrinsic value of a warrant can never be negative. By way of explanation:
if the price of the underlying instrument is at or below the exercise price, the intrinsic value of a call equals zero. In this instance, the price of the warrant consists only of “time value”. On the flipside, the intrinsic value of a put is equal to zero if the price of the underlying instrument is at or above the exercise price.
Time value
Once you’ve calculated the intrinsic value of a warrant, it’s also easy to figure out what the time value of that warrant is. You simply deduct the intrinsic value from the current market price of the warrant. In our example, the time value is equal to EUR 1.30 as you can see from the following calculation:
(warrant price – intrinsic value)
= (EUR 0.30 EUR – EUR 0.00)
= EUR 0.30
Time value gradually erodes during the term of a warrant and ultimately ends up at zero upon expiration. At that point, warrants with no intrinsic value expire worthless. Otherwise you can expect to receive payment of the intrinsic value. Take note, though: a warrant’s loss of time value accelerates during the final months of its term.
Premium
The premium indicates how much more expensive a purchase/sale of the underlying instrument would be via the purchase of a warrant and the immediate exercise of the option right as opposed to simply buying/selling the underlying instrument in the open market.
Hence the premium is a measure of how expensive a warrant actually is. It follows that, when given a choice between warrants with similar features, you should always buy the one with the lowest premium. By calculating the premium as an annualized percentage, warrants with different terms to expiry can be compared with each other.
The percentage premium for the call warrant in our example can be calculated as follows:
(strike price + warrant price / exercise ratio – share price) / share price * 100
= (EUR 30.00 + EUR 0.30 / 0.1 – EUR 30.00) / EUR 30.00 x 100
= 10 percent
Leverage
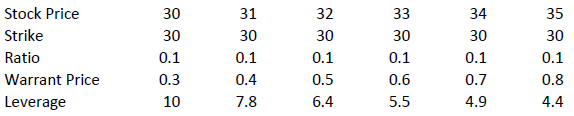
The amount of leverage is the price of the share * ratio divided by the price of the warrant. In our example 30.00*0.1/0.3 = 10. So when the price of ABC increases by 1% the value of the warrant increases by 10%.
The amount of leverage is not constant however; it varies as intrinsic and time value changes, and is particularly sensitive to changes in intrinsic value. As a rule of thumb, the higher the intrinsic value of the warrant, the lower the leverage. For example (assuming constant time value):