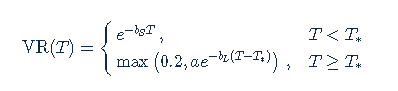VR(T) time decay and term adjusted Vega columns in Risk Navigator (SM)
Background
Risk Navigator (SM) has two Adjusted Vega columns that you can add to your report pages via menu Metrics → Position Risk...: "Adjusted Vega" and "Vega x T-1/2". A common question is what is our in-house time function that is used in the Adjusted Vega column and what is the aim of these columns. VR(T) is also generally used in our Stress Test or in the Risk Navigator custom scenario calculation of volatility index options (i.e VIX).
Abstract
Implied volatilities of two different options on the same underlying can change independently of each other. Most of the time the changes will have the same sign but not necessarily the same magnitude. In order to realistically aggregate volatility risk across multiple options into a single number, we need an assumption about relationship between implied volatility changes. In Risk Navigator, we always assume that within a single maturity, all implied volatility changes have the same sign and magnitude (i.e. a parallel shift of volatility curve). Across expiration dates, however, it is empirically known that short term volatility exhibits a higher variability than long term volatility, so the parallel shift is a poor assumption. This document outlines our approach based on volatility returns function (VR(T)). We also describe an alternative method developed to accommodate different requests.
VR(T) time decay
We applied the principal component analysis to study daily percentage changes of volatility as a function of time to maturity. In that study we found that the primary eigen-mode explains approximately 90% of the variance of the system (with second and third components explaining most of the remaining variance being the slope change and twist). The largest amplitude of change for the primary eigenvector occurs at very short maturities, and the amplitude monotonically decreases as time to expiration increase. The following graph shows the main eigenvector as a function of time (measured in calendar days). To smooth the numerically obtained curve, we parameterize it as a piecewise exponential function.
Functional Form: Amplitude vs. Calendar Days
To prevent the parametric function from becoming vanishingly small at long maturities, we apply a floor to the longer term exponential so the final implementation of this function is:
where bS=0.0180611, a=0.365678, bL=0.00482976, and T*=55.7 are obtained by fitting the main eigenvector to the parametric formula.
Inverse square root time decay
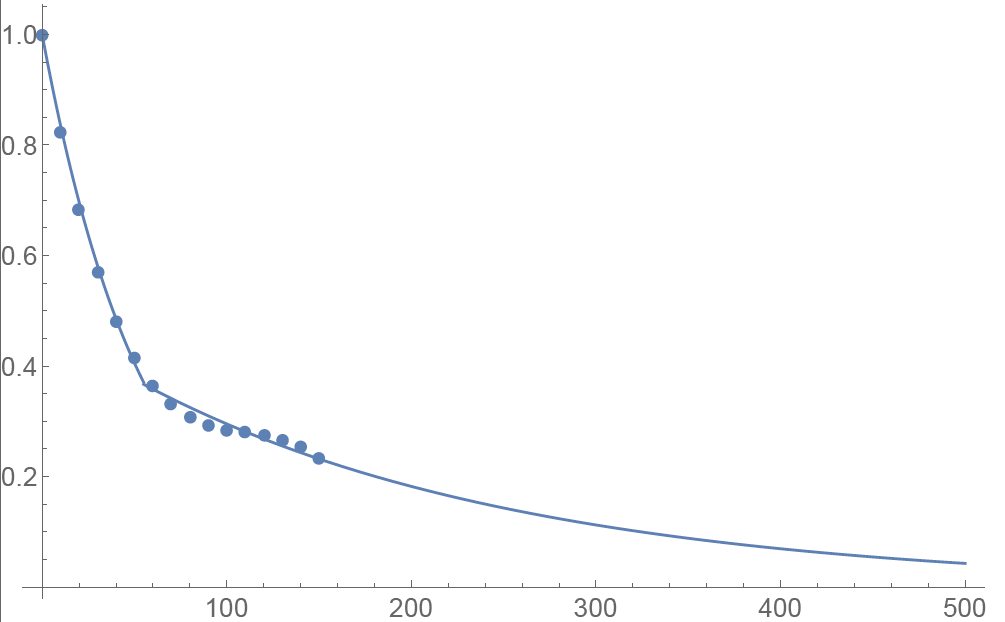
Another common approach to standardize volatility moves across maturities uses the factor 1/√T. As shown in the graph below, our house VR(T) function has a bigger volatility changes than this simplified model.
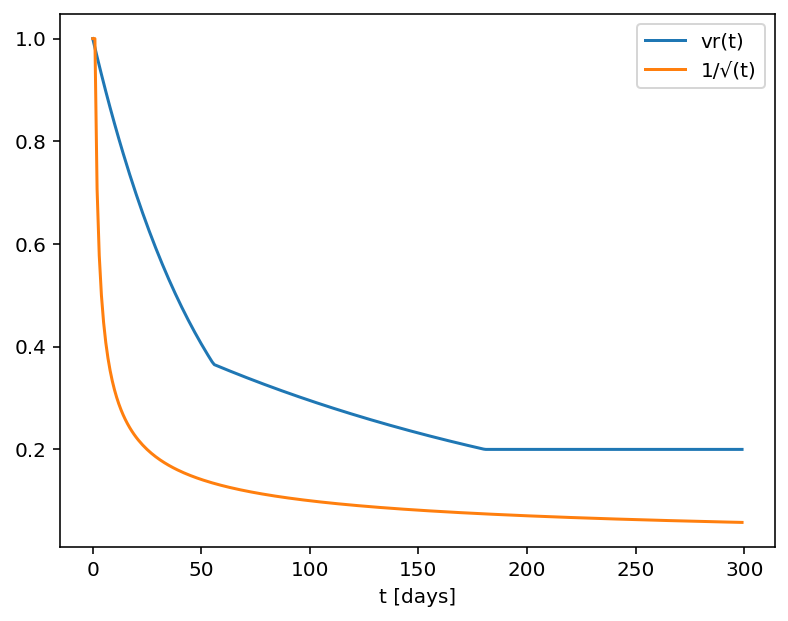
Time function comparison: Amplitude vs. Calendar Days
Adjusted Vega columns
Risk Navigator (SM) reports a computed Vega for each position; by convention, this is the p/l change per 1% increase in the volatility used for pricing. Aggregating these Vega values thus provides the portfolio p/l change for a 1% across-the-board increase in all volatilities – a parallel shift of volatility.
However, as described above a change in market volatilities might not take the form of a parallel shift. Empirically, we observe that the implied volatility of short-dated options tends to fluctuate more than that of longer-dated options. This differing sensitivity is similar to the "beta" parameter of the Capital Asset Pricing Model. We refer to this effect as term structure of volatility response.
By multiplying the Vega of an option position with an expiry-dependent quantity, we can compute a term-adjusted Vega intended to allow more accurate comparison of volatility exposures across expiries. Naturally the hoped-for increase in accuracy can only come about if the adjustment we choose turns out to accurately model the change in market implied volatility.
We offer two parametrized functions of expiry which can be used to compute this Vega adjustment to better represent the volatility sensitivity characteristics of the options as a function of time to maturity. Note that these are also referred as 'time weighted' or 'normalized' Vega.
Adjusted Vega
A column titled "Vega Adjusted" multiplies the Vega by our in-house VR(T) term structure function. This is available any option that is not a derivative of a Volatility Product ETP. Examples are SPX, IBM, VIX but not VXX.
Vega x T-1/2
A column for the same set of products as above titled "Vega x T-1/2" multiplies the Vega by the inverse square root of T (i.e. 1/√T) where T is the number of calendar days to expiry.
Aggregations
Cross over underlying aggregations are calculated in the usual fashion given the new values. Based on the selected Vega aggregation method we support None, Straight Add (SA) and Same Percentage Move (SPM). In SPM mode we summarize individual Vega values multiplied by implied volatility. All aggregation methods convert the values into the base currency of the portfolio.
Custom scenario calculation of volatility index options
Implied Volatility Indices are indexes that are computed real-time basis throughout each trading day just as a regular equity index, but they are measuring volatility and not price. Among the most important ones is CBOE's Marker Volatility Index (VIX). It measures the market's expectation of 30-day volatility implied by S&P 500 Index (SPX) option prices. The calculation estimates expected volatility by averaging the weighted prices of SPX puts and calls over a wide range of strike prices.
The pricing for volatility index options have some differences from the pricing for equity and stock index options. The underlying for such options is the expected, or forward, value of the index at expiration, rather than the current, or "spot" index value. Volatility index option prices should reflect the forward value of the volatility index (which is typically not as volatile as the spot index). Forward prices of option volatility exhibit a "term structure", meaning that the prices of options expiring on different dates may imply different, albeit related, volatility estimates.
For volatility index options like VIX the custom scenario editor of Risk Navigator offers custom adjustment of the VIX spot price and it estimates the scenario forward prices based on the current forward and VR(T) adjusted shock of the scenario adjusted index on the following way.
- Let S0 be the current spot index price, and
- S1 be the adjusted scenario index price.
- If F0 is the current real time forward price for the given option expiry, then
- F1 scenario forward price is F1 = F0 + (S1 - S0) x VR(T), where T is the number of calendar days to expiry.
在哪裡可以瞭解更多有關期權的信息?
期權清算公司(OCC)是所有美國交易所交易之證券期權的中央清算機構,其運營著一個呼叫中心以滿足個人投資者和零售證券經紀商的學習需求。其主要解決由OCC清算之期權產品的下列相關問題:
- 期權行業協會有關研討會、視頻和教學材料的信息;
- 基本期權問題,如期限定義和產品信息;
- 策略和操作性問題(包括特定交易頭寸和策略)解答。
可撥打1-800-OPTIONS聯繫呼叫中心。營業時間為美國中部標準時間週一至週四上午8點到下午5點,週五上午8點到下午4點.每月逢週五到期日營業時間將延長至下午5點。
到期前行使看漲期權的注意事項
簡介
到期前行使股票看漲期權通常不會帶來收益,因為:
- 這會導致剩餘期權時間價值的丟失;
- 需要更大的資金投入以支付股票交割;並且
- 會給期權持有人帶來更大的損失風險。
儘管如此,對於有能力滿足更高資金或借款要求并能承受更大下行市場風險的帳戶持有人來說,提前行使美式看漲期權行可獲取即將分派的股息。
背景
看漲期權持有人無權獲取底層股票的股息,因為該股息屬於股息登記日前的股票持有人所有。其他條件相同,股價應下降,降幅與除息日的股息保持一致。期權定價理論提出看漲期權價格將反映預期股息的折扣價格,看漲期權價格也可能在除息日下跌。最可能促成該情境與提前行權決定的條件如下:
1. 期權為深度價內期權,且Delta值為100;
2. 期權幾乎沒有時間價值;
3. 股息相對較高,且除息日在期權到期日之前。
舉例
為闡述這些條件對提前行權決定的影響,假設帳戶的多頭現金餘額為$9,000美元,且持有行使價為$90.00美元的ABC多頭看漲頭寸,10天后到期。ABC當前成交價為$100.00美元,每股股息為$2.00美元,明天是除息日。再假設期權價格和股票價格走勢相同,且在除息日下跌的幅度均為股息金額。
這裡,我們將檢查行權決定,目的是維持100股delta頭寸并使用兩種期權價格假設(一個為平價,一個高於平價)最大化總資產。
情境 1:期權價格為平價 - $10.00美元
如果期權以平價交易,提前行權可維持delta頭寸并可避免股票除息交易時多頭期權價值遭到損失,從而保護資產。在這裡現金收入被全數用於以行使價購買股票,期權權利金就此喪失,並且股票(扣除股息)與應收股息會記入帳戶。如果您想通過在除息日前賣出期權并買入股票來達到同樣的效果,請記得考慮佣金/價差:
| 情境 1 | ||||
|
帳戶組成部份 |
起始餘額 |
提前行權 |
無行動 |
賣期權 & 買股票 |
| 現金 | $9,000 | $0 | $9,000 | $0 |
| 期權 | $1,000 | $0 | $800 | $0 |
| 股票 | $0 | $9,800 | $0 | $9,800 |
| 應收股息 | $0 | $200 | $0 | $200 |
| 總資產 | $10,000 | $10,000 | $9,800 | $10,000減去佣金/價差 |
情境 2:期權價格高於平價 - $11.00美元
如果期權以高於平價的價格交易,提前行權獲取股息則可能並不會帶來收益。在此情境中,提前行權可能會導致期權時間價值損失$100美元,而賣出期權買入股票在扣除佣金之後收益情況也可能不如不採取行動。在這裡,可取的行動為無行動。
| 情境 2 | ||||
| 帳戶組成部份 | 起始餘額 | 提前行權 | 無行動 |
賣期權 & 買股票 |
| 現金 | $9,000 | $0 | $9,000 | $100 |
| 期權 | $1,100 | $0 | $1,100 | $0 |
| 股票 | $0 | $9,800 | $0 | $9,800 |
| 應收股息 | $0 | $200 | $0 | $200 |
| 總資產 | $10,100 | $10,000 | $10,100 | $10,100減去佣金/價差 |
![]() 請注意:考慮到空頭期權邊被行權的可能性,持有作為價差組成部分之多頭看漲頭寸的賬戶持有人應格外注意不行使多頭期權邊的風險。請注意,空頭看漲期權的被行權會導致空頭股票頭寸,且在股息登記日前持有空頭股票頭寸的持有人有義務向股票的借出者支付股息。此外,清算所行權通知處理週期不支持提交響應被行權的行權通知。
請注意:考慮到空頭期權邊被行權的可能性,持有作為價差組成部分之多頭看漲頭寸的賬戶持有人應格外注意不行使多頭期權邊的風險。請注意,空頭看漲期權的被行權會導致空頭股票頭寸,且在股息登記日前持有空頭股票頭寸的持有人有義務向股票的借出者支付股息。此外,清算所行權通知處理週期不支持提交響應被行權的行權通知。
例如,假設SPDR S&P 500 ETF Trust (SPY)的信用看漲(熊市)價差包括100張13年3月到期行使價為$146美元的空頭合約,以及100張13年3月到期行使價為$147美元的多頭合約。在13年3月14日,SPY Trust宣布每股股息為$0.69372美元,並且會在13年4月30日向13年3月19日前登記的股東支付。因為美國股票的結算週期為3個工作日,想要獲取股息,交易者需要在13年1月14日之前買入股票或行使看漲期權,因為該日期一過,股票便開始除息交易。

13年3月14日,距離期權到期只剩一個交易日,平價成交的兩張期權合約每張合約的最大風險為$100美元,100張合約則為$10,000美元。但是,未能行使多頭合約以獲取股息以及未能避免空頭合約被其他想要獲取股息的交易者行權會使每張合約產生額外$67.372美元的風險,如果所有空頭看漲合約都被行權,則所有頭寸總風險為$6,737.20美元。如下表所示,如果空頭期權邊沒有被行權,則13年3月15日確定最終的合約結算價格時,最大風險仍為每張合約$100美元。
| 日期 | SPY收盤價 | 3月13日行使價為$146美元的看漲期權 | 3月13日行使價為$147美元的看漲期權 |
| 2013年3月14日 | $156.73 | $10.73 | $9.83 |
| 2013年3月15日 | $155.83 | $9.73 | $8.83 |
請注意,如果您的賬戶符合美國871(m)預扣稅要求,則除息日前平倉頭多期權頭寸並在除息日後重新建倉可能會帶來收益。
有關如何提交提前通知的信息請查看IB網站。
上方內容僅作信息參考,不構成任何推薦或交易建議,也不代表提前行權會成功或適合所有客戶或交易。帳戶持有人應諮詢稅務專家以確定提前行權可能帶來的稅務影響,并應格外注意以多頭股票頭寸替換多頭期權頭寸的潛在風險。
Considerations for Exercising Call Options Prior to Expiration
INTRODUCTION
Exercising an equity call option prior to expiration ordinarily provides no economic benefit as:
- It results in a forfeiture of any remaining option time value;
- Requires a greater commitment of capital for the payment or financing of the stock delivery; and
- May expose the option holder to greater risk of loss on the stock relative to the option premium.
Nonetheless, for account holders who have the capacity to meet an increased capital or borrowing requirement and potentially greater downside market risk, it can be economically beneficial to request early exercise of an American Style call option in order to capture an upcoming dividend.
BACKGROUND
As background, the owner of a call option is not entitled to receive a dividend on the underlying stock as this dividend only accrues to the holders of stock as of its dividend Record Date. All other things being equal, the price of the stock should decline by an amount equal to the dividend on the Ex-Dividend date. While option pricing theory suggests that the call price will reflect the discounted value of expected dividends paid throughout its duration, it may decline as well on the Ex-Dividend date. The conditions which make this scenario most likely and the early exercise decision favorable are as follows:
1. The option is deep-in-the-money and has a delta of 100;
2. The option has little or no time value;
3. The dividend is relatively high and its Ex-Date precedes the option expiration date.
EXAMPLES
To illustrate the impact of these conditions upon the early exercise decision, consider an account maintaining a long cash balance of $9,000 and a long call position in hypothetical stock “ABC” having a strike price of $90.00 and time to expiration of 10 days. ABC, currently trading at $100.00, has declared a dividend of $2.00 per share with tomorrow being the Ex-Dividend date. Also assume that the option price and stock price behave similarly and decline by the dividend amount on the Ex-Date.
Here, we will review the exercise decision with the intent of maintaining the 100 share delta position and maximizing total equity using two option price assumptions, one in which the option is selling at parity and another above parity.
SCENARIO 1: Option Price At Parity - $10.00
In the case of an option trading at parity, early exercise will serve to maintain the position delta and avoid the loss of value in long option when the stock trades ex-dividend, to preserve equity. Here the cash proceeds are applied in their entirety to buy the stock at the strike, the option premium is forfeited and the stock (net of dividend) and dividend receivable are credited to the account. If you aim for the same end result by selling the option prior to the Ex-Dividend date and purchasing the stock, remember to factor in commissions/spreads:
| SCENARIO 1 | ||||
|
Account Components |
Beginning Balance |
Early Exercise |
No Action |
Sell Option & Buy Stock |
| Cash | $9,000 | $0 | $9,000 | $0 |
| Option | $1,000 | $0 | $800 | $0 |
| Stock | $0 | $9,800 | $0 | $9,800 |
| Dividend Receivable | $0 | $200 | $0 | $200 |
| Total Equity | $10,000 | $10,000 | $9,800 | $10,000 less commissions/spreads |
SCENARIO 2: Option Price Above Parity - $11.00
In the case of an option trading above parity, early exercise to capture the dividend may not be economically beneficial. In this scenario, early exercise would result in a loss of $100 in option time value, while selling the option and buying the stock, after commissions, may be less beneficial than taking no action. In this scenario, the preferable action would be No Action.
| SCENARIO 2 | ||||
|
Account Components |
Beginning Balance |
Early Exercise |
No Action |
Sell Option & Buy Stock |
| Cash | $9,000 | $0 | $9,000 | $100 |
| Option | $1,100 | $0 | $1,100 | $0 |
| Stock | $0 | $9,800 | $0 | $9,800 |
| Dividend Receivable | $0 | $200 | $0 | $200 |
| Total Equity | $10,100 | $10,000 | $10,100 | $10,100 less commissions/spreads |
![]() NOTE:
NOTE:
Options have two components that make up their total premium value - intrinsic value and time value. The intrinsic value is the amount by which the option is in-the-money, while the time value represents the possibility that the option could become even more profitable before expiration as the underlying asset price fluctuates while providing protection against adverse moves.
Many options are American-style, which means they can be exercised early, ahead of their expiration date. Early exercise of an option eliminates the remaining time value component from the option's premium, since the option holder loses protection against unfavorable movements in the underlying asset’s price.
This makes early exercise suboptimal in most situations, as the option holder is willingly forfeiting a portion of the option's value.
There are a few specific circumstances where early exercise could make sense, such as:
- For call options on a stock that will pay dividends soon, where the dividend amount exceeds the remaining time value (and only if the exercise will settle on or prior to the record date for the dividend).
- For deep in-the-money options where the time value is negligible compared to the intrinsic value, and the option is expected to drop in value due to interest rate effects (PUTS), or expected stock loan benefits (CALLS).
The first case, exercising an in the money call immediately ahead of a dividend payment, is the most common economically-sensible early exercise. In most cases, it is advisable to hold or sell the option instead of exercising it early, in order to capture the remaining time value. An option should only be exercised early after carefully considering all factors and determining that the benefits of early exercise outweigh the time value being surrendered.
Account holders holding a long call position as part of a spread should pay particular attention to the risks of not exercising the long leg given the likelihood of being assigned on the short leg. Note that the assignment of a short call results in a short stock position and holders of short stock positions as of a dividend Record Date are obligated to pay the dividend to the lender of the shares. In addition, the clearinghouse processing cycle for exercise notices does not accommodate submission of exercise notices in response to assignment.
As example, consider a credit call (bear) spread on the SPDR S&P 500 ETF Trust (SPY) consisting of 100 short contracts in the March '13 $146 strike and 100 long contracts in the March '13 $147 strike. On 3/14/13, with the SPY Trust declared a dividend of $0.69372 per share, payable 4/30/13 to shareholders of record as of 3/19/13. Given the 3 business day settlement time frame for U.S. stocks, one would have had to buy the stock or exercise the call no later than 3/14/13 in order receive the dividend, as the next day the stock began trading Ex-Dividend.

On 3/14/13, with one trading day left prior to expiration, the two option contracts traded at parity, suggesting maximum risk of $100 per contract or $10,000 on the 100 contract position. However, the failure to exercise the long contract in order to capture the dividend and protect against the likely assignment on the short contracts by others seeking the dividend created an additional risk of $67.372 per contract or $6,737.20 on the position representing the dividend obligation were all short calls assigned. As reflected on the table below, had the short option leg not been assigned, the maximum risk when the final contract settlement prices were determined on 3/15/13 would have remained at $100 per contract.
| Date | SPY Close | March '13 $146 Call | March '13 $147 Call |
| March 14, 2013 | $156.73 | $10.73 | $9.83 |
| March 15, 2013 | $155.83 | $9.73 | $8.83 |
Please note that if your account is subject to tax withholding requirements of the US Treasure rule 871(m), it may be beneficial to close a long option position before the ex-dividend date and re-open the position after ex-dividend.
For information regarding how to submit an early exercise notice please click here.
The above article is provided for information purposes only as is not intended as a recommendation, trading advice nor does it constitute a conclusion that early exercise will be successful or appropriate for all customers or trades. Account holders should consult with a tax specialist to determine what, if any, tax consequences may result from early exercise and should pay particular attention to the potential risks of substituting a long option position with a long stock position.
Where can I receive additional information on options?
The Options Clearing Corporation (OCC), the central clearinghouse for all US exchange traded securities option, operates a call center to serve the educational needs of individual investors and retail securities brokers. The resource will address the following questions and issues related to OCC cleared options products:
- Options Industry Council information regarding seminars, video and educational materials;
- Basic options-related questions such as definition of terms and product information;
- Responses to strategic and operational questions including specific trade positions and strategies.
The call center can be reached by dialing 1-800-OPTIONS. The hours of operation are Monday through Thursday from 8 a.m. to 5 p.m. (CST) and Friday from 8 a.m. to 4 p.m. (CST). Hours for the monthly expiration Friday will be extended to 5 p.m. (CST).