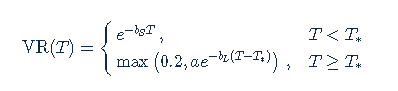VR(T) time decay and term adjusted Vega columns in Risk Navigator (SM)
Background
Risk Navigator (SM) has two Adjusted Vega columns that you can add to your report pages via menu Metrics → Position Risk...: "Adjusted Vega" and "Vega x T-1/2". A common question is what is our in-house time function that is used in the Adjusted Vega column and what is the aim of these columns. VR(T) is also generally used in our Stress Test or in the Risk Navigator custom scenario calculation of volatility index options (i.e VIX).
Abstract
Implied volatilities of two different options on the same underlying can change independently of each other. Most of the time the changes will have the same sign but not necessarily the same magnitude. In order to realistically aggregate volatility risk across multiple options into a single number, we need an assumption about relationship between implied volatility changes. In Risk Navigator, we always assume that within a single maturity, all implied volatility changes have the same sign and magnitude (i.e. a parallel shift of volatility curve). Across expiration dates, however, it is empirically known that short term volatility exhibits a higher variability than long term volatility, so the parallel shift is a poor assumption. This document outlines our approach based on volatility returns function (VR(T)). We also describe an alternative method developed to accommodate different requests.
VR(T) time decay
We applied the principal component analysis to study daily percentage changes of volatility as a function of time to maturity. In that study we found that the primary eigen-mode explains approximately 90% of the variance of the system (with second and third components explaining most of the remaining variance being the slope change and twist). The largest amplitude of change for the primary eigenvector occurs at very short maturities, and the amplitude monotonically decreases as time to expiration increase. The following graph shows the main eigenvector as a function of time (measured in calendar days). To smooth the numerically obtained curve, we parameterize it as a piecewise exponential function.
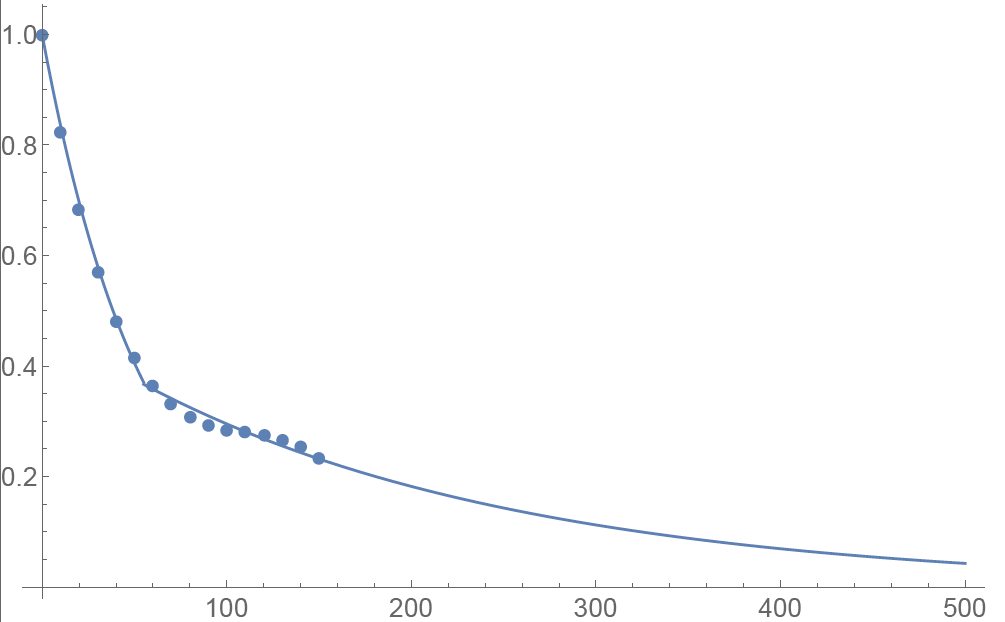
Functional Form: Amplitude vs. Calendar Days
To prevent the parametric function from becoming vanishingly small at long maturities, we apply a floor to the longer term exponential so the final implementation of this function is:
where bS=0.0180611, a=0.365678, bL=0.00482976, and T*=55.7 are obtained by fitting the main eigenvector to the parametric formula.
Inverse square root time decay
Another common approach to standardize volatility moves across maturities uses the factor 1/√T. As shown in the graph below, our house VR(T) function has a bigger volatility changes than this simplified model.
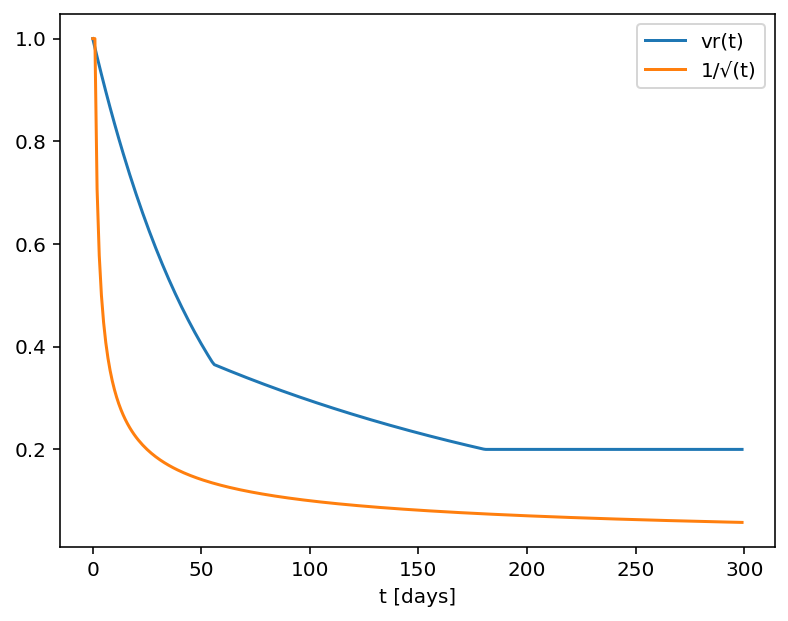
Time function comparison: Amplitude vs. Calendar Days
Adjusted Vega columns
Risk Navigator (SM) reports a computed Vega for each position; by convention, this is the p/l change per 1% increase in the volatility used for pricing. Aggregating these Vega values thus provides the portfolio p/l change for a 1% across-the-board increase in all volatilities – a parallel shift of volatility.
However, as described above a change in market volatilities might not take the form of a parallel shift. Empirically, we observe that the implied volatility of short-dated options tends to fluctuate more than that of longer-dated options. This differing sensitivity is similar to the "beta" parameter of the Capital Asset Pricing Model. We refer to this effect as term structure of volatility response.
By multiplying the Vega of an option position with an expiry-dependent quantity, we can compute a term-adjusted Vega intended to allow more accurate comparison of volatility exposures across expiries. Naturally the hoped-for increase in accuracy can only come about if the adjustment we choose turns out to accurately model the change in market implied volatility.
We offer two parametrized functions of expiry which can be used to compute this Vega adjustment to better represent the volatility sensitivity characteristics of the options as a function of time to maturity. Note that these are also referred as 'time weighted' or 'normalized' Vega.
Adjusted Vega
A column titled "Vega Adjusted" multiplies the Vega by our in-house VR(T) term structure function. This is available any option that is not a derivative of a Volatility Product ETP. Examples are SPX, IBM, VIX but not VXX.
Vega x T-1/2
A column for the same set of products as above titled "Vega x T-1/2" multiplies the Vega by the inverse square root of T (i.e. 1/√T) where T is the number of calendar days to expiry.
Aggregations
Cross over underlying aggregations are calculated in the usual fashion given the new values. Based on the selected Vega aggregation method we support None, Straight Add (SA) and Same Percentage Move (SPM). In SPM mode we summarize individual Vega values multiplied by implied volatility. All aggregation methods convert the values into the base currency of the portfolio.
Custom scenario calculation of volatility index options
Implied Volatility Indices are indexes that are computed real-time basis throughout each trading day just as a regular equity index, but they are measuring volatility and not price. Among the most important ones is CBOE's Marker Volatility Index (VIX). It measures the market's expectation of 30-day volatility implied by S&P 500 Index (SPX) option prices. The calculation estimates expected volatility by averaging the weighted prices of SPX puts and calls over a wide range of strike prices.
The pricing for volatility index options have some differences from the pricing for equity and stock index options. The underlying for such options is the expected, or forward, value of the index at expiration, rather than the current, or "spot" index value. Volatility index option prices should reflect the forward value of the volatility index (which is typically not as volatile as the spot index). Forward prices of option volatility exhibit a "term structure", meaning that the prices of options expiring on different dates may imply different, albeit related, volatility estimates.
For volatility index options like VIX the custom scenario editor of Risk Navigator offers custom adjustment of the VIX spot price and it estimates the scenario forward prices based on the current forward and VR(T) adjusted shock of the scenario adjusted index on the following way.
- Let S0 be the current spot index price, and
- S1 be the adjusted scenario index price.
- If F0 is the current real time forward price for the given option expiry, then
- F1 scenario forward price is F1 = F0 + (S1 - S0) x VR(T), where T is the number of calendar days to expiry.
¿Dónde puedo recibir información adicional sobre opciones?
La Options Clearing Corporation (OCC), la cámara de compensación para todas las opciones sobre acciones cotizadas en bolsa en EE. UU., opera un centro de atención telefónica para cumplir con las necesidades de formación de los inversores individuales y los brókeres de valores minoristas. Este recurso responderá a las siguientes cuestiones y asuntos relacionados con los productos de opciones compensados por la OCC:
- Información del Options Industry Council sobre seminarios, vídeos y material educativo;
- Preguntas básicas relacionadas con opciones, como la definición de términos e información sobre productos;
- La respuesta a preguntas estratégicas y operativas, las cuales incluyen posiciones y estrategias de negociación específicas.
Puede comunicarse al centro de atención telefónica a través del 1-800-OPTIONS (solo para EE. UU.). El horario de negociación es de lunes a jueves de 8:00 a 17:00 h y viernes de 8:00 a 16:00 h (hora estándar del centro, CST). El horario para el vencimiento mensual de los viernes se extenderá hasta las 17:00 h (hora estándar del centro, CST).
Consideraciones para ejercitar opciones call antes del vencimiento
INTRODUCCIÓN
El ejercicio de una opción call antes del vencimiento no proporciona, normalmente, un beneficio económico, ya que:
- Tiene como resultado la pérdida de cualquier valor temporal de la opción que quede;
- Requiere una mayor inversión de capital para el pago o financiación de la entrega de acciones; y
- Puede exponer al titular de la opción a un mayor riesgo de pérdida sobre la acción en relación con la prima de la opción.
Aún así, para titulares de cuenta que tengan la capacidad de cumplir los requisitos de préstamo o de aumento de capital y de hacer frente a un riesgo potencialmente mayor de caída del mercado, puede ser económicamente beneficioso solicitar un ejercicio temprano de una opción call de tipo americano para capturar un próximo dividendo.
TRASFONDO
Como trasfondo, el titular de una opción call no tiene derecho a recibir un dividendo de la acción subyacente ya que este dividendo solo se devenga para los titulares de acciones en la fecha de cierre de registro de su dividendo. En igualdad de condiciones, el precio de la acción debería decaer en una cantidad igual al dividendo en la fecha ExDividendo. Aunque la teoría del precio de opciones sugiere que el precio call reflejará el valor descontado de los dividendos esperados pagados durante su duración, es posible que decline en la fecha exdividendo. Las condiciones que convierten este escenario en más probable y que hacen más favorable la decisión de un ejercicio temprano son las siguientes:
1. La opción está muy en dinero y tiene una delta de 100;
2. La opción no tiene valor temporal o tiene muy poco;
3. El dividendo es relativamente elevado y su fecha ex precede a la fecha de vencimiento de la opción.
EJEMPLOS
Para ilustrar el impacto de estas condiciones sobre una decisión de ejercicio temprano, consideremos una cuenta que mantenga un saldo en efectivo largo de 9,000 USD y una posición de call larga en un valor hipotético “ABC”, con un precio de ejecución de 90.00 USD y un tiempo hasta vencimiento de 10 días. ABC, que actualmente opera a 100.00 USD, ha declarado un dividendo de 2.00 USD por acción, siendo mañana la fecha exdividendo. También asumiremos que el precio de opción y el precio de acción se comportan de forma similar y declinan según la cantidad de dividendo en la fecha ex.
Aquí, revisaremos la decisión de ejercicio con la intención de mantener la posición de delta de 100 y maximizar la liquidez total mediante dos asunciones de precio de opción; una en la que la opción se vende a la par y otra sobre la par.
ESCENARIO 1: precio de opción a la par - 10.00 USD
En el caso de una opción que opere a la par, el ejercicio temprano servirá para mantener la delta de la posición y evitar la pérdida de valor en la opción larga cuando la acción opere exdividendo. Aquí, el producto en efectivo se aplica en su totalidad a la compra de la acción al precio de ejercicio, la prima de la opción se pierde y la acción, neta de dividendo, y el dividendo pendiente de pago se acreditan en la cuenta. Si busca el mismo resultado al vender la opción antes de la fecha ex dividendo y comprar la acción, recuerde que debe factorizar las comisiones/diferenciales:
| ESCENARIO 1 | ||||
|
Componentes de cuenta |
Saldo inicial |
Ejercicio temprano |
No actuar |
Vender opción y comprar acción |
| Efectivo | $9,000 | $0 | $9,000 | $0 |
| Opción | $1,000 | $0 | $800 | $0 |
| Acción | $0 | $9,800 | $0 | $9,800 |
| Dividendo por cobrar | $0 | $200 | $0 | $200 |
| Liquidez total | $10,000 | $10,000 | $9,800 | $10,000 menos comisiones/diferenciales |
ESCENARIO 2: precio de opción sobre la par - 11.00 USD
En el caso de una opción que opere sobre la par, el ejercicio temprano para capturar el dividendo podría no ser económicamente beneficioso. En este escenario, el ejercicio temprano tendría como resultado una pérdida de 100 USD en valor temporal de la acción, mientras que la venta de la opción y la compra de la acción, después de pagar comisiones, podría ser menos beneficiosa que no realizar ninguna acción. En este escenario, la acción preferible habría sido No actuar.
| ESCENARIO 2 | ||||
|
Componentes de cuenta |
Saldo inicial |
Ejercicio temprano |
No actuar |
Vender opción y comprar acción |
| Efectivo | $9,000 | $0 | $9,000 | $100 |
| Opción | $1,100 | $0 | $1,100 | $0 |
| Acción | $0 | $9,800 | $0 | $9,800 |
| Dividendo pendiente de pago | $0 | $200 | $0 | $200 |
| Liquidez total | $10,100 | $10,000 | $10,100 | $10,100 menos comisiones/diferenciales |
![]() NOTA: los titulares de cuenta que mantengan una posición call larga como parte de un diferencial deberían prestar particular atención al riesgo de no ejercitar el tramo largo dada la posibilidad de que se asigne en el tramo corto. Hay que tener en cuenta que la asignación de una opción call corta tiene como resultado una posición corta en acciones y los titulares de posiciones cortas en acciones en la fecha de registro del dividendo están obligados a pagar el dividendo al prestador de las acciones. Además, el ciclo de procesamiento de la cámara de contratación para notificaciones de ejercicio no acepta entregas de notificaciones de ejercicio como respuesta a la asignación.
NOTA: los titulares de cuenta que mantengan una posición call larga como parte de un diferencial deberían prestar particular atención al riesgo de no ejercitar el tramo largo dada la posibilidad de que se asigne en el tramo corto. Hay que tener en cuenta que la asignación de una opción call corta tiene como resultado una posición corta en acciones y los titulares de posiciones cortas en acciones en la fecha de registro del dividendo están obligados a pagar el dividendo al prestador de las acciones. Además, el ciclo de procesamiento de la cámara de contratación para notificaciones de ejercicio no acepta entregas de notificaciones de ejercicio como respuesta a la asignación.
Como ejemplo, consideremos un diferencial de opción call de crédito (bajista) para SPDR S&P 500 ETF Trust (SPY) que consista en 100 contratos cortos al precio de ejercicio de 146 USD en marzo de 2013 y 100 contratos largos al precio de ejercicio de 147 USD en marzo de 2013. El 14 de marzo de 2013, el SPY Trust declaró un dividendo de 0.69372 USD por acción, pagadero el 30 de abril de 2013 a los accionistas registrados a fecha del 19 de marzo de 2013. Dado el periodo de tres días hábiles para la liquidación para acciones estadounidenses, habría que haber comprado la acción el 14 de marzo de 2013 a más tardar, para recibir el dividendo, ya que al día siguiente la acción empezó a operar exdividendo.

El 14 de marzo de 2013, con un día de negociación previo al vencimiento, los dos contratos de opciones operaron a la par, lo que sugiere el riesgo máximo de 100 USD por contrato o 10,000 USD en la posición de100 contratos. Sin embargo, el no ejercitar el contrato largo para capturar el dividendo y protegerse frente a la probable asignación de los contratos cortos por parte de aquellos que buscaran el dividendo creó un riesgo adicional de 67.372 USD por contrato o 6,737.20 USD en la posición que represente la obligación de dividendo una vez asignadas todas las call cortas. Como se ve en la tabla siguiente, si el tramo de la opción corta no se hubiera asignado, el riesgo máximo cuando se determinaron los precios de liquidación del contrato final el 15 de marzo de 2013 habría permanecido en 100 USD por contrato.
| Fecha | Cierre SPY | Marzo '13, $146 Call | Marzo '13, $147 Call |
| 14 de marzo, 2013 | $156.73 | $10.73 | $9.83 |
| 15 de marzo, 2013 | $155.83 | $9.73 | $8.83 |
Por favor, tenga en cuenta que si su cuenta está sujeta a requisitos de retenciones fiscales bajo la norma 871(m) del Tesoro estadounidense, podría ser beneficioso cerrar una posición larga en opciones antes de la fecha exdividendo y reabrir la posición después de la fecha exdividendo.
Para más información sobre cómo enviar una notificación de ejercicio temprano, por favor haga clic aquí.
El artículo anterior se proporciona solo con propósitos informativos, y no se considera una recomendación, consejos operativos ni constituye una conclusión de que el ejercicio temprano tendrá éxito o será adecuado para todos los cliente so todas las operaciones. Los titulares de cuenta deberían consultar con un especialista fiscal para determinar las consecuencias fiscales, si las hubiere, de un ejercicio temprano y deberían prestar particular atención a los riesgos potenciales de sustituir una posición en opciones larga por una posición en acciones corta.
Considerations for Exercising Call Options Prior to Expiration
INTRODUCTION
Exercising an equity call option prior to expiration ordinarily provides no economic benefit as:
- It results in a forfeiture of any remaining option time value;
- Requires a greater commitment of capital for the payment or financing of the stock delivery; and
- May expose the option holder to greater risk of loss on the stock relative to the option premium.
Nonetheless, for account holders who have the capacity to meet an increased capital or borrowing requirement and potentially greater downside market risk, it can be economically beneficial to request early exercise of an American Style call option in order to capture an upcoming dividend.
BACKGROUND
As background, the owner of a call option is not entitled to receive a dividend on the underlying stock as this dividend only accrues to the holders of stock as of its dividend Record Date. All other things being equal, the price of the stock should decline by an amount equal to the dividend on the Ex-Dividend date. While option pricing theory suggests that the call price will reflect the discounted value of expected dividends paid throughout its duration, it may decline as well on the Ex-Dividend date. The conditions which make this scenario most likely and the early exercise decision favorable are as follows:
1. The option is deep-in-the-money and has a delta of 100;
2. The option has little or no time value;
3. The dividend is relatively high and its Ex-Date precedes the option expiration date.
EXAMPLES
To illustrate the impact of these conditions upon the early exercise decision, consider an account maintaining a long cash balance of $9,000 and a long call position in hypothetical stock “ABC” having a strike price of $90.00 and time to expiration of 10 days. ABC, currently trading at $100.00, has declared a dividend of $2.00 per share with tomorrow being the Ex-Dividend date. Also assume that the option price and stock price behave similarly and decline by the dividend amount on the Ex-Date.
Here, we will review the exercise decision with the intent of maintaining the 100 share delta position and maximizing total equity using two option price assumptions, one in which the option is selling at parity and another above parity.
SCENARIO 1: Option Price At Parity - $10.00
In the case of an option trading at parity, early exercise will serve to maintain the position delta and avoid the loss of value in long option when the stock trades ex-dividend, to preserve equity. Here the cash proceeds are applied in their entirety to buy the stock at the strike, the option premium is forfeited and the stock (net of dividend) and dividend receivable are credited to the account. If you aim for the same end result by selling the option prior to the Ex-Dividend date and purchasing the stock, remember to factor in commissions/spreads:
| SCENARIO 1 | ||||
|
Account Components |
Beginning Balance |
Early Exercise |
No Action |
Sell Option & Buy Stock |
| Cash | $9,000 | $0 | $9,000 | $0 |
| Option | $1,000 | $0 | $800 | $0 |
| Stock | $0 | $9,800 | $0 | $9,800 |
| Dividend Receivable | $0 | $200 | $0 | $200 |
| Total Equity | $10,000 | $10,000 | $9,800 | $10,000 less commissions/spreads |
SCENARIO 2: Option Price Above Parity - $11.00
In the case of an option trading above parity, early exercise to capture the dividend may not be economically beneficial. In this scenario, early exercise would result in a loss of $100 in option time value, while selling the option and buying the stock, after commissions, may be less beneficial than taking no action. In this scenario, the preferable action would be No Action.
| SCENARIO 2 | ||||
|
Account Components |
Beginning Balance |
Early Exercise |
No Action |
Sell Option & Buy Stock |
| Cash | $9,000 | $0 | $9,000 | $100 |
| Option | $1,100 | $0 | $1,100 | $0 |
| Stock | $0 | $9,800 | $0 | $9,800 |
| Dividend Receivable | $0 | $200 | $0 | $200 |
| Total Equity | $10,100 | $10,000 | $10,100 | $10,100 less commissions/spreads |
![]() NOTE:
NOTE:
Options have two components that make up their total premium value - intrinsic value and time value. The intrinsic value is the amount by which the option is in-the-money, while the time value represents the possibility that the option could become even more profitable before expiration as the underlying asset price fluctuates while providing protection against adverse moves.
Many options are American-style, which means they can be exercised early, ahead of their expiration date. Early exercise of an option eliminates the remaining time value component from the option's premium, since the option holder loses protection against unfavorable movements in the underlying asset’s price.
This makes early exercise suboptimal in most situations, as the option holder is willingly forfeiting a portion of the option's value.
There are a few specific circumstances where early exercise could make sense, such as:
- For call options on a stock that will pay dividends soon, where the dividend amount exceeds the remaining time value (and only if the exercise will settle on or prior to the record date for the dividend).
- For deep in-the-money options where the time value is negligible compared to the intrinsic value, and the option is expected to drop in value due to interest rate effects (PUTS), or expected stock loan benefits (CALLS).
The first case, exercising an in the money call immediately ahead of a dividend payment, is the most common economically-sensible early exercise. In most cases, it is advisable to hold or sell the option instead of exercising it early, in order to capture the remaining time value. An option should only be exercised early after carefully considering all factors and determining that the benefits of early exercise outweigh the time value being surrendered.
Account holders holding a long call position as part of a spread should pay particular attention to the risks of not exercising the long leg given the likelihood of being assigned on the short leg. Note that the assignment of a short call results in a short stock position and holders of short stock positions as of a dividend Record Date are obligated to pay the dividend to the lender of the shares. In addition, the clearinghouse processing cycle for exercise notices does not accommodate submission of exercise notices in response to assignment.
As example, consider a credit call (bear) spread on the SPDR S&P 500 ETF Trust (SPY) consisting of 100 short contracts in the March '13 $146 strike and 100 long contracts in the March '13 $147 strike. On 3/14/13, with the SPY Trust declared a dividend of $0.69372 per share, payable 4/30/13 to shareholders of record as of 3/19/13. Given the 3 business day settlement time frame for U.S. stocks, one would have had to buy the stock or exercise the call no later than 3/14/13 in order receive the dividend, as the next day the stock began trading Ex-Dividend.

On 3/14/13, with one trading day left prior to expiration, the two option contracts traded at parity, suggesting maximum risk of $100 per contract or $10,000 on the 100 contract position. However, the failure to exercise the long contract in order to capture the dividend and protect against the likely assignment on the short contracts by others seeking the dividend created an additional risk of $67.372 per contract or $6,737.20 on the position representing the dividend obligation were all short calls assigned. As reflected on the table below, had the short option leg not been assigned, the maximum risk when the final contract settlement prices were determined on 3/15/13 would have remained at $100 per contract.
| Date | SPY Close | March '13 $146 Call | March '13 $147 Call |
| March 14, 2013 | $156.73 | $10.73 | $9.83 |
| March 15, 2013 | $155.83 | $9.73 | $8.83 |
Please note that if your account is subject to tax withholding requirements of the US Treasure rule 871(m), it may be beneficial to close a long option position before the ex-dividend date and re-open the position after ex-dividend.
For information regarding how to submit an early exercise notice please click here.
The above article is provided for information purposes only as is not intended as a recommendation, trading advice nor does it constitute a conclusion that early exercise will be successful or appropriate for all customers or trades. Account holders should consult with a tax specialist to determine what, if any, tax consequences may result from early exercise and should pay particular attention to the potential risks of substituting a long option position with a long stock position.
Where can I receive additional information on options?
The Options Clearing Corporation (OCC), the central clearinghouse for all US exchange traded securities option, operates a call center to serve the educational needs of individual investors and retail securities brokers. The resource will address the following questions and issues related to OCC cleared options products:
- Options Industry Council information regarding seminars, video and educational materials;
- Basic options-related questions such as definition of terms and product information;
- Responses to strategic and operational questions including specific trade positions and strategies.
The call center can be reached by dialing 1-800-OPTIONS. The hours of operation are Monday through Thursday from 8 a.m. to 5 p.m. (CST) and Friday from 8 a.m. to 4 p.m. (CST). Hours for the monthly expiration Friday will be extended to 5 p.m. (CST).